Sadly, many people do not realize that even if the majority of those who engage in behavior X belong to category Y, that does not mean that the majority of people in category Y engage in X. This point is often made, rightly, with respect to race and violent crime and religion and terror. But most treatments I’ve seen either imply that anyone who doesn’t understand is a moron, or manage to scare away the target audience by throwing in a pile of math without explaining it. In this post, I’ll try to actually explain why we can’t conclude that most members of Y are prone to acts of X even if most acts of X are committed by members of Y. This post won’t insult anyone for being unfamiliar with Bayes’ Theorem, nor will you find much algebra herein. I’m just going to try to explain, with a relative minimum of technical detail, why we can’t assume that most members of Y engage in behavior X just because most people who engage in X are members of Y.
Let’s start with a simple example, one free of political baggage.
Suppose that some drug test is known to yield positives 98% of the time when the subject is in fact a user of the drug in question, and negatives 98% of the time when they are not. That is, the risk of a false positive is quite low, at only 2%. (As is the risk of a false negative, though we’re not concerned about that here.) What is the probability that an individual who tests positive is in fact a user of the drug?
That’s a trick question. We can’t answer it without knowing the baseline rate of usage in the population. And therein lies the rub — if the drug is commonly used, then your gut intuition probably isn’t too far off the mark. But if it’s not, you may be surprised by the answer.
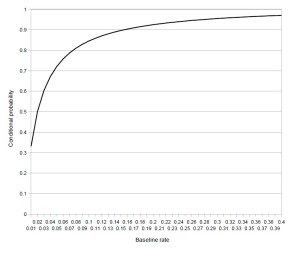
The following graph plots the conditional probability that an individual who tested positive for use of the drug is in fact a drug user as a function of the baseline rate of usage in the population, calculated via Bayes’ Theorem.
If at least 15% of the population uses the drug, the probability that an individual who tests positive in fact uses the drug will be over 90%. Thus, if you were to erroneously conflate the likelihood of a true positive with the actual probability that the person is a user of the drug, that wouldn’t be too egregious a mistake. But if the baseline rate of usage is only 1%, a positive result only implies a 33% chance that the person uses the drug. And that’s with a very accurate test! (You can rest assured that the methods used by the FBI and the NSA to sniff out terrorists leave room for more than a 2% chance of a false positive.)
How can that be? Suppose we randomly grab 100 people off the streets and force them all to take our drug test (which would be totally feasible, ethical, and legal). Statistically, 1 of them is going to be a user, and they’ll almost certainly test positive. But odds are two other people will as well, because the test only gives us the right answer 98% of the time. So we’ll have three positive results, but only one drug user. (That was’t so bad, was it? Anyway, I promise those are the last numbers you’ll see in this post.)
What does this tell us? Put simply, the probability that you’d be mistaken to assume that someone who belongs to group Y is likely to commit or have committed act X simply because most such acts are committed by members of group Y grows exponentially higher as X becomes rarer. The reason you should not assume that a person is a terrorist just because they’re Muslim, then, is not just that this is politically incorrect and likely to offend delicate liberal sensibilities. It’s that it’s almost certainly incorrect, full stop.
The following Venn diagram illustrates the point (please forgive my utter lack of artistic talent).
 The big circle on the left represents adherents of Islam. The one on the right represents Christianity. (For ease of exposition, I’m ignoring all other faiths, as well as variation within these categories. I’ve also made the circles the same size, implying that there are equal numbers of Christians and Muslims, whereas there are considerably more Christians in the world than Muslims.)
The big circle on the left represents adherents of Islam. The one on the right represents Christianity. (For ease of exposition, I’m ignoring all other faiths, as well as variation within these categories. I’ve also made the circles the same size, implying that there are equal numbers of Christians and Muslims, whereas there are considerably more Christians in the world than Muslims.)
The small circle in the middle represents those who have conducted, or are actively planning to conduct, acts of terrorism. For the sake of argument, I’ve assumed that the majority of terrorist acts are committed by Muslims (hence the better part of the circle appearing in light green), while only a small fraction are committed by Christians (and a tiny sliver of the middle circle light yellow). (If you’re having trouble with the notion of Christian terrorism, feel free to assume that the majority of these are committed by people who just so happen to be Christian but who were in fact motivated to kill by political concerns, such as separatism or nationalism or radical environmentalism or whatever. And if you don’t think the same can be said of terrorist attacks committed by people who just so happen to be Muslim, fine. The point I’m trying to make doesn’t depend on any particular assumptions about whether terrorist attacks committed by people of a certain religion are caused by their religious beliefs.)
What the diagram shows is a hypothetical world in which most people have never committed, and have no intention of committing, terrorist attacks. The probability that any given person is a terrorist is negligible, regardless of their faith, even though we have assumed that most terrorist attacks are committed by Muslims.
Of course, this diagram does not itself tell us anything about the likelihood that any given Muslim is planning a terrorist attack. It merely illustrates the point that it’s possible for most terrorists to be Muslim without most Muslims being terrorists. So it’s worth noting that various surveys indicate that the average Muslim is less likely than the average American or average Israeli to view violence against civilians as justifiable.
If you’re having trouble reconciling those survey results with the fact that most acts referred to as terrorists attacks by Western media are perpetrated by Muslims, you might want to go back and review the drug test example. And be thankful that terror attacks are rare enough for the risk of invalid inference to be so high.
I am an assistant professor of political science at the University at Buffalo, SUNY. I mostly write here about "rational choice" and IR theory. I also maintain my own blog, fparena.blogspot.com.

I don’t really get the first part about bayes’ theorem, in part because I don’t know the reasoning behind that asymptotic curve relationship.
As for second about invalid inference, I guess the most fundamental/introductory fallacy this boils down to is the “fallacy of illicit conversion”? The general form of the fallacy being “all Ps are Qs, therefore all Qs are Ps.”
Examples include: “all cats have ears, therefore everything having ears are cats.” Or “all Christians believe in a supreme being, all people believing in a supreme being are Christians.”
It’s fallacious because P could be a subset of Q, making “all Ps are Qs” correct but “all Qs are Ps wrong.”
I guess your post is a more advanced and developed version of this which takes into account set intersections and the ratio between the subset and the bigger set?
That’s a useful way to think about it, yes.
Bayes’ Theorem tells us the probability that A is true given that we’ve observed B. The graph is simply an application of this, where A is “uses the drug” and B is “tested positive for the drug”. The point I was trying to illustrate is that our initial estimate of how likely A is to be true is hugely important, particularly when it takes on small values. At large values of the initial probability, the answer Bayes’ Theorem gives us is close enough to what most people’s gut intuition is likely to be that it’s not really a big deal that most people don’t calculate probabilities using Bayes’ Theorem. At small values of the initial probability, the difference between what most people probably think is right and what logic tells us become really big. Basically, stereotypes are least accurate when they concern rare traits/behaviors. Such as terrorism.
This makes sense in principle. But, it appears to simple to me because people likely do not believe these events are ‘rare.’ People who stereotype African American wrt crime, for example, are likely to believe that they have committed many crimes during their lives (on jury duty recently, and this is borne out).
Those who stereotype Muslims in the most malicious ways are likely to believe that (a) Muslims are prone to terrorism, favor terrorism, or aid terrorists and (b) every terrorist attack committed by a Muslim will reinforce (a) [Let’s say through Bayes’ Rule]. Note that (a) is something that one can believe to be common: even though ‘few attacks are successful’, there may be people wanting and planning them. For this interpretation to work, in other words, people need to think that terrorist attacks–or more generally preferences consistent with terrorists–are rare, which I find suspect. Mueller would say ‘fear industry’ for example.
I should add I am talking about the American public’s perception. Terrorist preferences are clearly rare.
I assumed that was what you meant.
Fair point, Eric. I was arguing that people draw incorrect inferences from the information they have, but I think you are right to point out that the “information” they have is incorrect in the first place. It’ll only be once we get past the problem of threat inflation that we can begin to deal with the problem I identified in my post.
This is pretty much a new point, although its related.
Isn’t there also a potential problem because of the way we assign conditional probabilities? For example, if the prior probability that persons of group A who are anonymous to me are terrorists is x, and a new event occurs where an anonymous person from Group A commits a terrorist attack, then it would be rational on Bayes rule to infer a higher posterior probability?
If x is low and Bayes factor is pretty low, then of course its hard to get to the view that all A are terrorists, but it would increase. If its high–threat inflation–of course it would remain higher (and be higher).
I apologize then. I must have misunderstood you. I thought I was simply paraphrasing your original comment.
Yes, your posterior belief that any given member of Y is X increases when members of Y do X. But the difference should be very, very modest. Of course, in reality, people overweight recent and emotionally salient events, but if they were applying Bayes’ Theorem, their belief would be very modestly affected by any one incident.
You had the original point right. I had a new concern.
Gotcha. Thanks for clearing that up.
Put more simply, you may be right that inferences about individuals does not work in accord to Bayes’ rule. But, when dealing with populations, someone might confirm their understanding (the stereotype is ‘right’).
If one changes one’s beliefs about a large group of people by any substantial amount after observing the actions of one of its members, one is committing an inferential error. I don’t dispute that people do this. My point is that they are mistaken to do so. Beliefs about large populations should only be revised to any significant degree in response to information concerning the behavior of a non-trivial proportion thereof.
I agree with this. The crucial question is whether the stereotype is confirmed, which you are saying it has been. This makes the stereotype rational.
Why not rely on basic probabilities instead? Stereotypes of a population are only rational–in cases like this–when the probability of an individual being able to produce that event and the total number of individuals in the population is the same as the number of events.
So,if we assume that individuals have a .01% chance of successfully committing a terrorist attack in a ten year period, then we should see 160000 attacks in a decade given that the Muslim population is 1.6 billion (that was a wiki search). Since we do not see that number of attacks, clearly the stereotype is wrong.
This doesn’t require Bayes rule though..
I guess it depends on what you mean by “the stereotype”. My sense (from undergrads and poll data) is that many Americans believe that a very large proportion of Muslims are terrorists. That is not true, and terrorist attacks perpetrated by Muslims do virtually nothing to validate it. But if “the stereotype” means that most terrorist attacks are perpetrated by Muslims, that’s arguably true (though of course it depends on one’s definition of terrorism). An additional attack by Muslims would neither add nor detract much from the validity of this claim, though it could be interpreted as illustrative of it.
But, yes, you’re absolutely right that we don’t need Bayes’ Theorem to see that the proportion of Muslims who are terrorists must be extremely small. As you rightly note, the number of attacks we’ve seen is nowhere near what it would be otherwise. Applying Bayes’ Theorem is just one way of making the point. Ditto Venn diagrams.
Consider the additional fact that, to meet a Muslim terrorist, you need a Muslim, who is a terrorist, and who has not been caught. Ask your undergrads whether they think the government is good at that, and I’m pretty sure that “Muslim terrorism” will be a greater preoccupation for the fraction that thinks the government is doing a bad job at immigration and crime control. There’s more than one likelihood barrier to meeting a Muslim terrorist, so it really has to be a huge leap of indoctrinated faith to get that statement out. Politics is probably the art of having people claim such things.
Agreed on all points, Fr.
Somewhat off topic (if you dont mind) but do you have any recomendations on the best way (books/online courses etc) to teach yourself statistics..I’ve begun with coursera and The Cartoon book on stats (which is actually pretty good) so am looking to move on from there, but think the high end stuff (Gelmans book for example) is probably beyond me at this stage..(Ill go back and do the coursera course properly, but wondering are there any other decent programs..)
Once again, sorry for the off topic! (great post, btw)
That’s tough. It’s not an easy topic to teach yourself. There are a lot of really good books that make handy reference guides once you’re past a certain comfort level, but getting there isn’t easy.
I haven’t read it myself, but I’ve heard a lot of good things about the Freedman, Pisani, and Purves text. It might be worth checking out.
https://www.amazon.com/Statistics-David-Freedman/dp/8130915871/ref=sr_1_4?s=books&ie=UTF8&qid=1374845445&sr=1-4&keywords=freedman+statistics
Thanks Phil! I’m gonna order the book
Yeah I have less and less faith in my ability to learn it to any sort of competence, but Im happy to get the basics right at this stage
My pleasure, Ronan. I hope it’s useful!
See also (from Bill Easterly): https://aidwatchers.com/2011/03/the-congressional-muslim-terrorism-hearings-the-mathematical-witness-transcript/
That’s a great post, Ryan.
The post seems to be based on the fallacy that all mistakes are equally costly — that just because a conclusion is “almost certainly incorrect, full stop” it should not be made. But that’s obviously not true.
https://www.tdaxp.com/archive/2013/07/26/stereotyping-and-rare-but-important-events.html
The policy recommendation you’ve assumed I offered could be said to be based on that fallacy. But the claim that one’s estimate of the probability that any given Muslim is a terrorist remains “almost certainly incorrect” even if a policy that accepts a risk of treating innocent people with suspicion is deemed justifiable. That’s a separate, if obviously related, discussion.
So if the test is only 98% accurate, how do you determine the “actual” prevalence in the population in the first place? For that matter, how do you determine that the test is 98% accurate if you don’t start off with a population that you know *with certainty* has a determinate prevalence, so you can apply the test and see how accurate it really is?
(I am asking this not to be obnoxious or to set a trap of some kind. I am asking because this is an aspect of Bayesian inference that has always puzzled me.)
Great questions, PTJ.
Any number used for the actual prevalence would necessarily be rough, I think, given the nature of the behavior involved. For the purposes of illustration, we can treat these things as straightforward, but in practice I’m sure they’re not. However, the estimates needn’t be based on the test itself. Survey research would play a big role, I imagine, and there’s a certain amount of information conveyed by the rate of overdoses, changes in street price after large drug busts, etc. Of course, the best that’ll give you is a set of reasonable upper and lower bounds. But, again, the (range of) estimate(s) could be derived independently of the test.
As for the accuracy rates, I’m not sure how this is done with actual drug tests. You certainly can’t do a lab experiment where you randomly assign some people placebos and others illicit substances.
Perhaps I should have used pregnancy tests as an example instead. :)
It’s the “in practice…they’re not” that confuses me. As a mathematical conclusion, Bayes’ Theorem seems straightforward. As a practical matter, though, I wonder whether we ever have sufficient information outside of the lab to make it work. How good an estimate for these probabilities (both the prior and the test accuracy) do we need?
Full disclosure, part of why I am asking this is because I have generally been just fine with a frequentist understanding of probability, which may be because I misunderstand the Bayesian position. So I am trying to see if I need to rationally update my position ;-)
I agree we’re unlikely to have precise estimates of the relevant inputs outside the lab much of the time. Not everything is as hard to get information about as illicit behavior, but, yeah, this is an issue. How accurate the figures need to be depends in part on their relative size. Being off by a few percentage points would seriously mislead you if you’re dealing with rare events, whereas being off by a fairly substantial margin would make relatively little difference if you’re talking about something that occurs pretty frequently. In other words, I think your concern is absolutely a valid one, but there are situations where it’s important.
That said, the problem of not knowing what the prior should be is a somewhat bigger issue for Bayesian statistics than many realize. The way most people try to get around it is by starting with “uninformative priors”, which are wrongly believed to be neutral. It doesn’t always make much of a difference, but there’s no way to get around the fact that assumptions must be made. There are statisticians who make this point (https://normaldeviate.wordpress.com/2013/07/13/lost-causes-in-statistics-ii-noninformative-priors/), but I’m not sure many political scientists are paying much attention.
Myself, I mostly only use Bayes’ Theorem for theoretical applications. I’m more interested in how it disciplines our reasoning when we take the inputs as given than I am in claiming it can tell us everything there is to know about the world.
And that is my favorite thing about this post by far.
(By “that” I mean Phil’s last paragraph in the comment above: the use of Bayes’ theorem to show how far off people’s intuitions can be.)
At the risk of sounding like a total neophyte, I would say that I prefer a Bayesian understanding for a few reasons. First, insofar as the universe is pretty deterministic (there’s some bounded stochasticity at the quantum level), there is only one future, and of the set of events which we think might be in that future, their probabilities are either 0 or 1. So this means that when we’re assessing the probably of some event, in reality we are assessing how probable we are to make a correct prediction if we predict its occurrence – in other words, an epistemic evaluation rather than a physical one, which better fits what I understand Bayesian probability to be. Second, Bayes’ Theorem seems to be a simple way to describe how people should rigorously update their beliefs in the face of new evidence. To do the maths, you need to quantify, but the principle itself works even without precise formalisations. This means that I can fit Bayesian probability within a broader theory of reasoning which is compatible with abductive inference and some general principles of good critical thinking. Third, the fact that, as Phil has pointed out, Bayesian probability is explicitly so extensively dependent on priors makes it easier to place probability calculations within the broader edifice of our beliefs about the world, which is methodologically good.
Interesting way of looking at things, Simon. I agree with you about incorporating new evidence, as Bayes’ Theorem is compatible with (indeed embodies) principles of good critical thinking, and also that it’s good to place probability calculations within a broader edifice of beliefs about the world. As to the point about the single future, though, I’m having a hard time seeing how that’s an argument for Bayesian versus frequentist interpretations of probability. Can frequentist calculations not also be viewed as estimates of how likely our predictions of the future are to be right?
They can! I thought about my point after posting it and realised this myself. I think I should rephrase it, though. I’m trying to distinguish between the probability of our predictions being right based on the probability of some event occurring, and it being based on how well we have inferred the determined future based on our interpretation of the evidence at hand. Am I correct in seeing this as the difference between frequentism and bayesianism? Because the former seems metaphysically problematic.
I think I see where you’re going, but frequentism and Bayesianism both seek to interpret the evidence at hand in order to estimate the probability of some event occurring, so there’s a better way to say it. The difference concerns what information counts, really.
One way to put it is that frequentists are more interested in what data-generating process would be most likely to give rise to the data at hand, irrespective of what they’ve seen in the past, whereas Bayesian approaches permit one to start from an arbitrary a priori expectation and then adjust that expectation in response to the evidence at hand. For example, if I were to flip a coin 10 times and observe 6 heads, a frequentist would say that the coin is more likely to be unfair than fair (albeit by a very small margin) while a Bayesian would say that we have reason to start with the assumption that a coin is very, very likely to be fair and would slightly revise that estimate based on the fact that we’re slightly more likely to see 6 heads from an unfair coin than a fair coin. (Actually, to be really careful with my words, I would wager that 99% of self-proclaimed frequentists would hesitate to say that the coin is even slightly more likely to be unfair than fair…but in so doing, they’d be implicitly applying Bayesian reasoning.)
I’ll confess that this statement doesn’t really make sense to me: ‘frequentism and Bayesianism both seek to interpret the evidence at hand
in order to estimate the probability of some event occurring’.
The prototypical example of Bayesian reasoning I usually encounter is that of a medical test. Given some known base rate of occurrence and of false results, how likely is it that the test result is accurate can be determined through Bayes’ Theorem. So in this case, it is not the probability of some event occurring that is being assessed, but the probability of some finding being true. We already know that the probability of that event is either 1 or 0. We are simply trying to decide which of the two we should conclude.
But this isn’t the case with frequentism, right? There it really is about the probability of the event occurring being somewhere between 0 and 1?
I should have chosen my words more carefully.
I think part of what’s adding to the confusion here is that Bayesian statistics and Bayesian reasoning are not synonymous. Bayesian statistics explicitly incorporates Bayesian reasoning into the process of estimating quantities of interest. Frequentist statistics does not. How one interprets the quantity of interest estimated through the statistical analysis is, technically, a separate question.
In some cases, we are interested in what has already occurred. In other cases, we are interested in what will occur. Sometimes we’re interested in discrete events, those that either have occurred (will occur) or have not (will not). Sometimes we’re interested in continuous variables (whose values has already been determined or will be determined in the future). Both frequentist and Bayesian statistics can be used to answer all of those questions.
The difference between them strictly concerns how (and whether) to incorporate baseline expectations into our attempt at estimating quantities of interest.
A nice metaphor I’ve seen used, which may help more than the coin flip example, is as follows:
You’ve lost your cell phone somewhere in your house. To find it, you ask your spouse/friend/someone/anyone to call it. A frequentist approach to finding your phone would be to walk all throughout the house, listening for the ringtone. A Bayesian approach would be to consider where you’ve found it in the past after misplacing it, start there, and then correct course based on where you hear the ringtone.
Okay, this is helpful for me. I was under the incorrect impression that frequentism assumed that the universe was actually stochastic, which made it seem much less reasonable than Bayesianism.
If I may press you further, why would we ever choose frequentism over Bayesianism? In your metaphor, for example, the Bayesian approach seems the wiser.
Good question. It’s probably not a great example for that reason. It illustrates the difference well, but it does make it hard to see why some favor frequentism.
The argument in favor of frequentism is that Bayesian statistics stack the deck in favor of the prior. When we have a good prior, using it as a baseline seems obviously useful. But sometimes we don’t. Or don’t know that we don’t. In those situations, frequentist statistics will allow us to accept the correct conclusion more readily, while a Bayesian model will, in a sense, require extraordinary evidence.
That’s the principled reason. The unsatisfying but all too often descriptively accurate one is that frequentist statistics is easier to learn and use. Many software packages are available that almost reduce the application of frequentist statistical analysis to point and click. Bayesian statistical analysis isn’t, at this point in time, so user-friendly.
The dirty secret no one discusses in public is that while your average quantoid is very proud of the fact that they’re “doing science” while the rest of the field ostensibly is not, the average quantoid also has no real understanding of what’s happening in their models. They’re basically typing “reg varname varname”, pressing enter, and then gazing at stars (for statistical significance). There are lots of exceptions, to be sure, but this is far more common than many are willing to admit. (Though, perhaps ironically, the first people to tell you that this approach to using statistics is dangerously widespread are those in the polmeth community — the high priests of quantitative analysis.) I approached quantitative analysis that way myself, once, I’m ashamed to say. And I see it all the time in friends/students/senior colleagues.
But you didn’t hear that from me.
(No one reads the 38th comment on a blog post, right?)
‘Gazing at stars’ is a cute way to put it, though not particularly flattering. While I succeeded in acquiring the basic skillset taught by my grad quant methods prof, with boast-worthy marks, I don’t really use associational analyses in my research. The only ‘quantoid’ I know well is in Michigan right now learning SEM, which seems more complicated than waterboarding your data for their secrets via basic regression models (with commensurate epistemic value). So perhaps I’ve managed to get a rosy picture of quant research?
It’s true that Stata is, literally, point-and-click. But regarding the principled reason, I’m not sure I understand what you’re saying – I think I sort of do, but would you give me an example of a situation in which there is a good methodological reason to prefer frequentist analysis?
No, it’s not particularly flattering. And in some cases, it’s not accurate either. But I’m afraid it is in some.
To return to the coin flip example, if you actually had a biased coin, you wouldn’t need a great deal of evidence to discover this using frequentist statistics. But the coin would need to either be very heavily weighted towards one side, or you’d need to observe deviation from 50% heads over a very large number of flips, before a Bayesian model would indicate that it was more likely to be biased than not. Basically, any time your prior (or range of priors if your’e averaging across many models, as is quite common) excludes the true value of the quantity of interest, you run a greater risk of arriving at the wrong conclusion using Bayesian statistics than frequentist statistics. The only time Bayesian approaches have a clear advantage is when there’s a strong prior that’s reasonably accurate.
That said, it’s worth noting that the two approaches often give the same answer. A lot of people are starting to say that the war between the two is really over blown and that it’s mostly just a matter of taste. I’m inclined to agree.
I see! It sounds as though it really just depends on the problem at hand, and is more about model selection than any kind of broader methodological commitment. Thanks for talking me through this!
I think a frequentist approach to the potentially biased coin would be to flip it often enough that the chances of the coin landing on heads more than on tails fell below some (admittedly, arbitrary, at least from the perspective of the math) level of significance. Since for a frequentist, “50% chance of heads” means “as the number of flips increases towards infinity, the frequency of ‘heads’ will approach half of the total number of flips,” the only way to empirically evaluate the proposition is to gather lots of data. So it seems like the applied Bayesian procedure is, largely, a way of making things more efficient in situations where we have sufficient information to do so. And then the interesting question is, when do we have sufficient information to do so?
Absolutely. The example was really stylized, because there’d be no reason to stop at ten flips. I was just using it to point out how the two approaches differ. When data is sparse (say, for example, the way some states get polled a few times a month during a presidential election while others don’t, leaving models like Nate Silver’s to predict the outcome for some states based mostly on the trend in national polling and the state’s demographics), Bayesian approaches rely on priors (sometimes for better and sometimes for worse) while frequentist approaches mostly just say “I got nuthin’ – could you gather more data please?”
I agree, the question is when we have sufficient information to do so. Reasonable people can (and do) disagree about that.
I just asked an someone about this, For illegal drug tests, there is usually a way to directly measure the use in the population. For example, you may go to a methadone clinic or trust user responses to surveys. Also, one can do direct blood draws where the presence of drugs may be more directly observable. This of course may only be one of the tests in a trial (and therefore have a smaller-n) but be worthwhile. In reality, because of the expense of doing these kinds of things, they often compare new tests to earlier tests, which has obvious problems.
Apparently the rules for false positives and false negatives are not so strict: they expect a range in the rates.
Interesting. Thanks for the information!
Thanks for the statistical explanation part — but my sense is that a lot of the people (like Dawkins) who talk about Muslims as terrorists are not making a primarily statistical argument anyway. (See, for example, this:
https://www.guardian.co.uk/world/2001/sep/15/september11.politicsphilosophyandsociety1)
Rather, they’re arguing about the content of the religion itself, as well as patterns of political socialization, and finally the ways in which people who are ‘religious’ think differently about risk and therefore about the risks associated with certain activities (such as dying in battle for one’s beliefs.) I suppose that explains why you’re not going to convince someone like Dawkins that his reasoning is faulty by pointing out that he did his statistical analysis incorrectly — and why you and he would probably reach such different policy recommendations based on your thinking.
I view those arguments as potential (perhaps even ad hoc) explanations for why we might expect the hypothesis to hold. But it doesn’t. Simple as that. That Dawkins continues to believe what he does in it in spite of all evidence to the contrary is somewhat ironic. I think you’re right that Dawkins is unlikely to change his mind, but it’s not because he as a valid point that renders the statistical reasoning irrelevant.
These arguments remind me of how people used to say Catholicism was incompatible with democracy. At the time that such arguments were all the rage, Spain and Portugal were authoritarian, as was most of Latin America, and what few examples there were of democratic states with majority Catholic populations (Ireland, Italy) had more than their share of problems. People argued that there was a reason for this, that Catholicism itself was inherently authoritarian. That Protestantism, at heart, was an attempt to wrest power away from the papacy and put it in the hands of the people, so of course majority Protestant states were more likely to be democratic. Then, lo and behold, Spain and Portugal democratized in the 70s, many of Latin American’s military dictatorships gave way to new democracies, and this argument lost prominence. There are still those who invoke it, but they aren’t taken as seriously as they once were. One can’t help but wonder if a few decades from now, if political circumstances in the Muslim world change, whether we’ll look back at arguments like Dawkins’ and cringe the same way we do claims that Catholicism is incompatible with democracy.
Or we could just start cringing now, and get a jump on things.
:)
Is Bayes enough? If whatever is at stake is significantly high(loss of life, property, fear of masses) then would the argument that 0.00007% of people of a faith are terrorists be adequate to justify treating everyone with the same yardstick?
If the likelihood of a Christian to be a terrorist is 0.000000007%, wouldnt that mean that the likelihood of a Muslim being a terrorist is 10000 times more than that of a Christian?
My justification despite understanding Bayes well also lies in attempting to minimize type-2 errors aka letting off a person who is a terrorist as not a terrorist. Read this https://statisticalexplanationoffearofislam.blogspot.in/ .
Lets not mix up the different functions of the “Court of Law” & “Law Enforcement”.
Stats is not shallow. Its not a puzzle.